- Computer Fundamentals Course
- Computer Fundamentals Tutorial
- Block Diagram of a Computer
- The Generation of Computers
- Types of Computers
- Classification of Computers
- Characteristics of Computers
- Applications of Computers
- Central Processing Unit
- Input Devices
- Output Devices
- Computer Memory and Types
- CD, HD, Floppy, and PenDrive
- Types of Computer Languages
- Types and Language Translator
- Number System with Types
- Decimal to Binary
- Decimal to Octal
- Decimal to Hexadecimal
- Binary to Decimal
- Binary to Octal
- Binary to Hexadecimal
- Octal to Decimal
- Octal to Binary
- Octal to Hexadecimal
- Hexadecimal to Decimal
- Hexadecimal to Binary
- Hexadecimal to Octal
- Algorithm and Flowchart
- Selection Sort
- Insertion Sort
- Bubble Sort
- Linear Search
- Binary Search
- Bitwise Operators
- Binary Number Addition
- EBCDIC & ASCII Code
- BCD, Excess-3, 2421, Gray Code
- Unicode Characters
BCD Code, Excess-3 Code, 2421 Codes, Gray Code
This article was written and is being distributed in order to provide a description of the four distinct sorts of codes, which are
Now that we have everything out of the way, let's go through each of these four codes one at a time, beginning with the "BCD code."
BCD Code
The BCD code is the most straightforward method for employing binary numbers to represent decimal numbers.
In BCD code, a decimal number is represented by a binary value that has four bits.
If a decimal number has two or more digits, then each of those digits is individually represented by its corresponding binary representation that has four bits. As an illustration, the number (278)10 written in BCD appears as seen in the following picture:
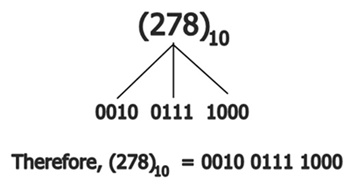
Therefore, we can say that the number 278 in binary is represented as 0010 0111 1000 or (278)10 = 0010 0111 1000.
BCD is a weighted code, which means that the weights of the binary bits that represent individual digits are 8, 4, and 1, respectively. Subtraction on modern computers is performed using complements, and it is difficult to construct complements when integers are represented using BCD codes.
However, we can also use a 4-bit binary value, which is called "BCD 8421 encoding." I included the following table for your understanding.
| Decimal digit | BCD | |||
|---|---|---|---|---|
| 8 | 4 | 2 | 1 | |
| 0 | 0 | 0 | 0 | 0 |
| 1 | 0 | 0 | 0 | 1 |
| 2 | 0 | 0 | 2 | 0 |
| 3 | 0 | 0 | 1 | 1 |
| 4 | 0 | 1 | 0 | 0 |
| 5 | 0 | 1 | 0 | 1 |
| 6 | 0 | 1 | 1 | 0 |
| 7 | 0 | 1 | 1 | 1 |
| 8 | 1 | 0 | 0 | 0 |
| 9 | 1 | 0 | 0 | 1 |
If you're not sure how the data is entering the table, let me explain briefly. To write the "8421" code for the matching "decimal digit," divide the decimal digit so that it comprises only 8, 4, 2, and 1, the sum of which is the decimal digit itself. For example, if 9 is divided into two digits, 8 and 1, there will be 1 in place of these two digits, and if we add 8 and 1, we will obtain 9. Another example is the number 7, which can be divided into three digits: 4, 2, and 1. As a result, we must write 1 under 4, 2, and 1.
If we want to convert 35 to BCD-8421 code, we can do so by remembering that 3 is equivalent to 0011, and 5 is equivalent to 1010, so 35 will be 00110101 in BCD-8421.
Excess-3 Code
In the excess-3 code, 3 is added to each individual digit of a decimal number, and then the binary equivalent is written. For example, the code (278)10 in excess-3 is represented by 0101101011. This code is not weighted.
Because 3 is added, the decimal digit "-3" equals "0000" in "Excess-3". For your understanding, I included the following table, which consists of decimal digits and their corresponding excess-3 codes.
| Decimal | Excess-3 |
|---|---|
| -3 | 0000 |
| -2 | 0001 |
| -1 | 0010 |
| 0 | 0011 |
| 1 | 0100 |
| 2 | 0101 |
| 3 | 0110 |
| 4 | 0111 |
| 5 | 1000 |
| 6 | 1001 |
| 7 | 1010 |
| 8 | 1011 |
| 9 | 1100 |
| 10 | 1101 |
| 11 | 1110 |
| 12 | 1111 |
If we take the example of converting 9 to "excess-3" code, Then, since 9 is equivalent to 1001, adding 3 gives 1100. Therefore, the decimal digit 9 is equivalent to 1100 in "excess-3." If you are still having trouble understanding it, let's take a look at the following process:
1001 (9) + 0011 (3) ---------- 1100
That is, the binary equivalent of 9 is 1001, but since we need to add the 3 in "excess-3," we must add 0011 (the equivalent value of 3) to 1001, which is 1100.
Other names of the "Excess-3" code are "3-excess" and "10-excess-3."
2421 Code
The 2421 code, which is also known as the "Aiken code," is another BCD code. It is a code that has been weighed. For example, 6 is 1100, and 3 is 0011.
The following table, which I have included in this section, is provided for your understanding.
| Decimal digit | 2 | 4 | 2 | 1 |
|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 |
| 1 | 0 | 0 | 0 | 1 |
| 2 | 0 | 0 | 1 | 0 |
| 3 | 0 | 0 | 1 | 1 |
| 4 | 0 | 1 | 0 | 0 |
| 5 | 1 | 0 | 1 | 1 |
| 6 | 1 | 1 | 0 | 0 |
| 7 | 1 | 1 | 0 | 1 |
| 8 | 1 | 1 | 1 | 0 |
| 9 | 1 | 1 | 1 | 1 |
I don't believe this table requires any further explanation after describing the "BCD-8421 code" using the table included in the "BCD code" section above. This table works similarly to that one.
GRAY Code
The gray code is a binary code. The binary bits are arranged in such a way that only one binary bit changes at a time when we change from any number to the next.
Gray code is reflected code. This code is used in shaft encodes, which indicate the angular position of a shaft in digital form. Shaft position encoder discs are used as sensors. It is not a weighted code. Gray code can be constructed using the following properties:
- A 1-bit gray code has two code words to represent the decimal numbers 0 and 1, respectively.
- A n-bit gray code will have the first 2n-1 gray codes for n-1 bits written in order with a leading 0 appended.
- The last 2n-1 gray code will be equal to the gray code words of an (n-1) bit gray code, written in reverse order (assuming a mirror is placed between the first 2n-1 and last 2n-1 gray codes) with a leading 1 appended.
Example
The following table provides an illustration of how each of the four distinct types of code can be transformed into the others.
| Decimal No. | BCD (8421) | Excess-3 Code | 2421 Code | Gray Code |
|---|---|---|---|---|
| 0 | 0000 | 0011 | 0000 | 0000 |
| 1 | 0001 | 0100 | 0001 | 0001 |
| 2 | 0010 | 0101 | 0010 | 0011 |
| 3 | 0011 | 0110 | 0011 | 0010 |
| 4 | 0100 | 0111 | 0100 | 0110 |
| 5 | 0101 | 1000 | 0101 | 0111 |
| 6 | 0110 | 1001 | 1100 | 0101 |
| 7 | 0111 | 1010 | 1101 | 0100 |
| 8 | 1000 | 1011 | 1110 | 1100 |
| 9 | 1001 | 1100 | 1111 | 1101 |
| 10 | 0001 0000 | 1101 | 1111 | |
| 11 | 0001 0001 | 1110 | 1110 | |
| 12 | 0001 0010 | 1111 | 1010 | |
| 13 | 0001 0011 | 1011 | ||
| 14 | 0001 0100 | 1001 | ||
| 15 | 0001 0101 | 1000 |
« Previous Tutorial Next Tutorial »